Future Value of a Single Amount (Practice Quiz)

Print PDF

For multiple-choice and true/false questions, simply press or click on what you think is the correct answer. For fill-in-the-blank questions, press or click on the blank space provided.

If you have difficulty answering the following questions, learn more about this topic by reading our Future Value of a Single Amount (Explanation).


  1. 1. The amount at a later point in time is known as a
    __________
    future
    value.
  2. 2.
    __________
    Compound (or Compounded)
    interest refers to earning interest on previously earned interest.
  3. 3. The amounts contained in a future value of 1 table for various combinations of n and i are referred to as future value
    __________
    factors
    .
  4. 4. In the future value of 1 table, n refers to the number of
    __________
    periods
    of time, such as months, quarters, years.
  5. 5. If you know the future value of a single deposit, the interest rate, and the number of periods that the interest is compounded, you will be able to calculate the
    __________
    present
    value by using a future value of 1 table.
  6. 6. Assume that you are calculating the future value of a single deposit by using a future value of 1 table. The deposit will be invested in an account earning 12% per year for four years. If the interest will be compounded quarterly, the number of periods (n) will be
    __________
    16 (4 years X 4 quarters per year)
    and i will be 3%.
  7. 7. An unrestricted deposit of $1,000 grows to a future value of $5,000 through the compounding of interest. Under the accrual basis of accounting, the $4,000 of growth should be reported as
    __________
    Interest Revenue (or Interest Income)
    .
  8. 8.

    Under the accrual basis of accounting, the interest earned over a three-year period on a single deposit should be reported on a company's income statement

    At The End Of 3 Years
    Wrong.
    During The 3 Years
    Right!
    Under the Accrual basis of accounting, revenues should be reported when they are earned. In this case, the interest revenue is earned in each of the three years.
    When Deposit Is Made
    Wrong.
  9. 9.

    Which compounding of an 8% annual interest rate will result in a larger future value?

    2% Per Quarter
    Right!
    This will provide more future value because interest will be earned on interest after three months (instead of one year).
    8% Per Year
    Wrong.
    Interest will not be earning interest until after one year, whereas quarterly compounding will allow interest to be earned on interest after three months.
    No Difference
    Wrong.
  10. 10. If you know the present value of a single amount, the future value of that amount, and the number of periods that the interest will be compounded, you can calculate the
    __________
    interest rate
    .
  11. 11. When using the future value of 1 table to calculate the future value of a deposit earning 10% per year compounded semiannually, you would use a factor from the column headed
    __________
    5% (10% per year divided by 2 six-month periods per year)
    .
  12. 12. An account or deposit will earn 12% interest per year for two years. Assuming that you are using the future value of 1 table and the interest is compounded monthly, you will find the factor in the row where n is
    __________
    24 (2 years X 12 months per year)
    periods.
  13. 13. An account or deposit will earn 12% interest per year for two years. Assuming that you are using the future value of 1 table and that the interest is compounded monthly, you will find the factor in the column where i is
    __________
    1% (12% divided by 12 months per year)
    .
  14. Use the following future value of 1 factors for solving the remaining questions:

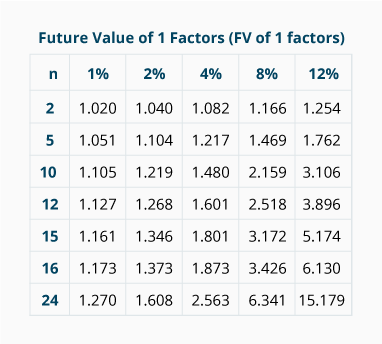
  15. 14. A deposit of $1,000 on January 1, 2023 will have a future value of $
    __________
    $1,469.
    FV of 1 = PV x FV of 1 factor for n = 5 years, i = 8% compounded annually
    FV of 1 = $1,000 x 1.469
    FV of 1 = $1, 469
    on December 31, 2027 (or January 1, 2028) if it is invested at 8% per year and the interest is compounded annually.
  16. 15. A deposit of $10,000 on January 1, 2023 will have a future value of $
    __________
    $14,800.
    FV of 1 = PV x FV of 1 factor for n = 10 semiannual periods, i = 4% per semiannual period
    FV of 1 = $10,000 x 1.480
    FV of 1 = $14,800
    on December 31, 2027 (or January 1, 2028) if it is invested at 8% per year and the interest is compounded semiannually.
  17. 16. A deposit of $2,000 on January 1, 2023 will have a future value of $
    __________
    $2,540.
    FV of 1 = PV x FV of 1 factor for n = 24 months, i = 1% per month
    FV of 1 = $2,000 x 1.270
    FV of 1 = $2,540
    on December 31, 2024 (or January 1, 2025) if it is invested at 12% per year and the interest is compounded monthly.
  18. 17. A deposit of $1,000 on January 1, 2023 will have a future value of $
    __________
    $1,373.
    FV of 1 = PV x FV of 1 factor for n = 16 quarters, i = 2% per quarter
    FV of 1 = $1,000 x 1.373
    FV of 1 = $1,373
    on December 31, 2026 (or January 1, 2027) if it is invested at 8% per year and the interest is compounded quarterly.
  19. 18. The interest rate that is necessary for a deposit of $1,000 to grow to $5,474 after 15 years of interest compounded annually is
    __________
    12%.
    FV of 1 = PV x FV of 1 factor for n = 15 years, i = ??% compounded yearly;
    $5,474 = $1,000 x FV of 1 factor for n = 15 yrs, i = ??% compounded yearly;
    5.474 = FV of 1 factor for n = 15 yrs, i = ??% compounded yearly;
    Look only in the row, n = 15, and locate the factor 5.474. It is in the column where i = 12%.
    % per year.
  20. 19. The annual interest rate that is necessary for a deposit of $1,000 to grow to $1,373 after four years of interest compounded quarterly is
    __________
    8%.
    FV of 1 = PV x FV of 1 factor for n = 16 quarters, i = ??% per quarter;
    $1,373 = $1,000 x FV of 1 factor for n = 16 qtrs, i = ??% per quarter;
    1.373 = FV of 1 factor for n = 16 qtrs, i = ??% per quarter;
    Look only in the row, n = 16, and locate the factor 1.373. It is in the column where i = 2%. This means that the rate per quarter is 2%. Since the question is asking for the annual rate, multiply the rate per quarter times 4 to arrive at 8% per year.
    % per year.
  21. 20. The number of years required for an investment of $1,000 to grow to $2,563 when invested at an annual rate of 8% compounded semiannually is
    __________
    12 years.
    FV of 1 = PV x FV of 1 factor for n = ?? six-month periods, i = 4% semiannually;
    $2,563 = $1,000 x FV of 1 factor for n = ?? six-month periods, i = 4% semiannually;
    2.563 = FV of 1 factor for n = ?? six-month periods, i = 4% semiannually;
    Look only in the column, i = 4%, and locate the factor 2.563. It is in the row where n = 24. This means that the number of six-month periods is 24, and that equals 12 years.
    years.

Want more practice questions?
Receive instant access to our graded Quick Tests (more than 1,800 unique test questions) when you join AccountingCoach PRO.
Mark the Practice Quiz as Complete

Future Value of a Single Amount Outline

0%
0
Certificate of Achievement

Certificates of Achievement

We now offer 10 Certificates of Achievement for Introductory Accounting and Bookkeeping. The certificates include Debits and Credits, Adjusting Entries, Financial Statements, Balance Sheet, Income Statement, Cash Flow Statement, Working Capital and Liquidity, Financial Ratios, Bank Reconciliation, and Payroll Accounting. Click here to learn more.

PRO Testimonial
"I am an engineer pursuing an MBA diploma and accounting & financial economics have been a huge challenge for me to overcome. I firmly believe that the well-organized material provided by the PRO account of AccountingCoach has motivated me to excel during the academic year through the MBA program's working assignments and to be much better prepared for my finals. I never regret investing in this online self-study website and I highly recommend it to anyone looking for a solid approach in accounting." - Michalis M.
How to Begin (Video)
Take the Tour