Mathematics of Future Value

The future value of a present amount can be expressed as:

We will illustrate how this mathematical expression works by using the amounts from the three accounts in Part 1.

Account #1: Annual Compounding

A single deposit of $10,000 will earn interest at 8% per year and the interest will be deposited at the end of one year. Since the interest is compounded annually, the one-year period can be represented by n = 1 and the corresponding interest rate will be i = 8% per year:

The formula shows that the present value of $10,000 will grow to the FV of $10,800 at the end of one year when interest of 8% is earned and the interest is added to the account only at the end of the year.

Account #2: Semiannual Compounding

In Account #2 the $10,000 deposit will earn interest at 8% per year, but the interest will be deposited at the end of each six-month period for one year. With semiannual compounding, the life of the investment is stated as n = 2 six-month periods. The interest rate per six-month period is i = 4% (8% annually divided by 2 six-month periods).

The present value of $10,000 will grow to a future value of $10,816 (rounded) at the end of two semiannual periods when the 8% annual interest rate is compounded semiannually.

Account #3: Quarterly Compounding

In Account #3 the $10,000 deposit will earn interest at 8% per year, but the interest earned will be deposited at the end of each three-month period for one year. With quarterly compounding, the life of the investment is stated as n = 4 quarterly periods. The annual interest rate is restated to be the quarterly rate of i = 2% (8% per year divided by 4 three-month periods).

The present value of $10,000 will grow to a future value of $10,824 (rounded) at the end of one year when the 8% annual interest rate is compounded quarterly.

Future Values for Greater Than One Year

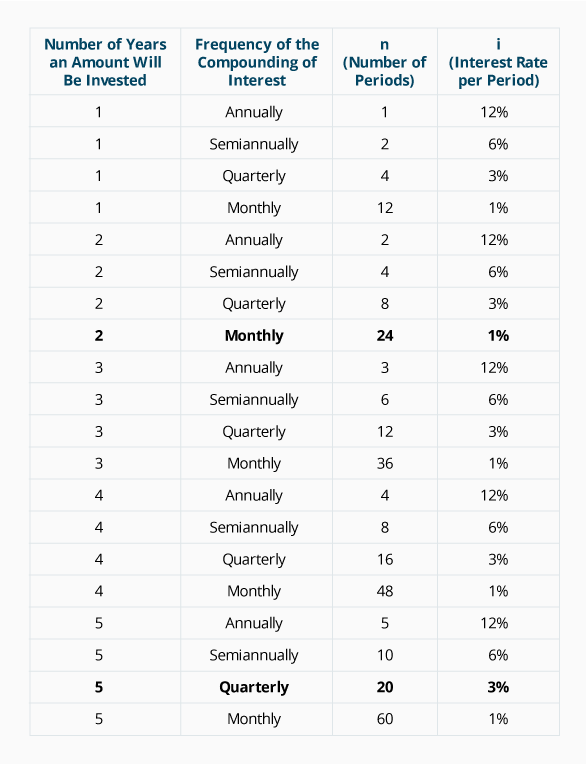
To be certain that you understand how the number of periods, n, and the interest rate, i, must be aligned with the compounding assumptions, we prepared the following chart. Note that the chart assumes an interest rate of 12% per year.

To be certain you understand the information in the chart, let’s assume that a single amount of $10,000 is deposited on January 1, 2024 and will remain in the account until December 31, 2028. This will mean a total of five years: 2024, 2025, 2026, 2027, and 2028. If the account will pay interest of 12% per year compounded quarterly, then n = 20 quarterly periods (5 years x 4 quarters per year), and i = 3% per quarter (12% per year divided by 4 quarters per year). The mathematical expression will be:

Let’s try one more example. Assume that a single amount of $10,000 is deposited on January 1, 2024 and will remain in the account until December 31, 2025 (a total of two years). If the account will pay interest of 12% per year compounded monthly, then n = 24 months (2 years x 12 months per year), and i = 1% per month (12% per year divided by 12 months per year). The mathematical expression will be: