Cash Flows

The company’s cash flows are not the same as the accounting net income amounts that are based on accrual accounting. The following table shows the cash received or saved as positive amounts, and the cash that was paid out or lost as negative amounts (in parentheses).

Nondiscounted Cash Flow Model

2. Payback. This method of evaluating business investments uses cash flows (not the accounting net income flows) to measure the amount of time it takes for a company to recoup its investment dollars.

There are two drawbacks to the payback model: (a) cash flows are not discounted for the time value of money, meaning that a dollar received three years from now has the same value as a dollar received in the current year, and (b) it fails to consider the profitability of the project in its entirety. For example, a project with a fast initial payback might not generate much profit over its life. Another project with a slow initial payback might be phenomenally profitable over its life because its profitability increases dramatically after the payback period.

Using the net cash flows before discounting in the table above, the payback period on the new machine for Treeline is 4.35 years:

Discounted Cash Flow Models

3. Net Present Value. This method of evaluating business investments estimates all of the cash flowing in and out of a project. The estimated cash flows are then discounted to the present to reflect the time value of money.

This technique is referred to as a discounted cash flow model or a present value model because it brings all of the estimated future cash amounts back to the present time. Using our Treeline Manufacturing example, the estimated cash flows in Year 5 will be discounted more than the estimated cash flows in Year 1 because cash received in the future is less valuable than cash received today.

Present value tables and financial calculators allow us to discount future cash amounts to the present time. Below is a portion of a present value table. It shows the value today (the present value) of receiving (or paying) one dollar at various points in time when the time value of money is 12%:

From this table you can see that if the time value of money is 12%, receiving $1.00 in ten years is equivalent to receiving $0.32 today.

In the net present value model the company must specify the rate it will use for discounting the future cash flows. (The rate selected will likely be the minimum that the company needs to earn on the project after uncertainties, risks, and the company’s cost of capital are considered.) The combination of the present value of the cash inflows and the present value of the cash outflows is known as the net present value.

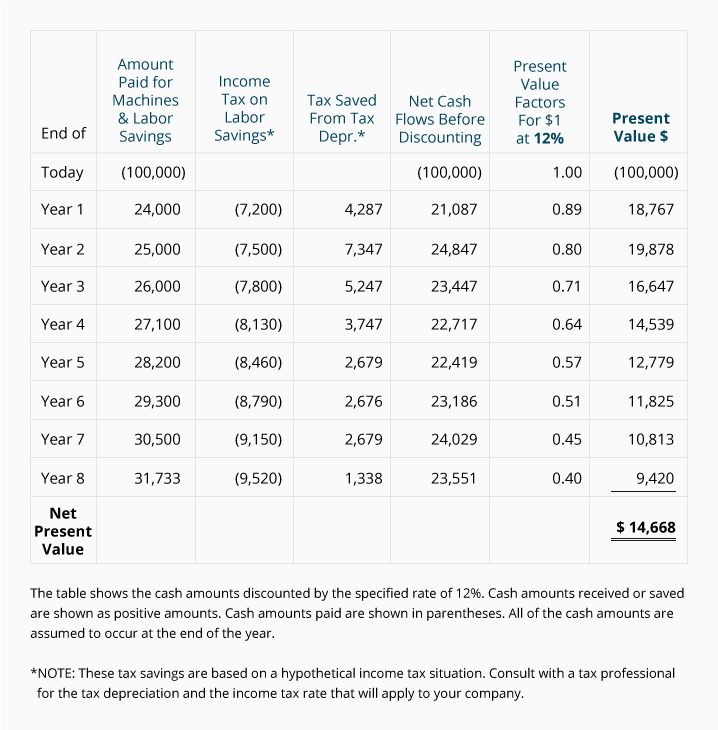
Assuming that Treeline chose to use a rate of 12%, let’s calculate the net present value of the relevant cash amounts for Treeline’s proposed purchase:

When the net present value is a positive amount, the project is earning more than the rate used to discount the cash flows. As you can see from the above table, Treeline’s proposed project is showing a positive net present value of $14,668. This means that the new machine will provide Treeline with $14,668 more in present value dollars than the minimum specified return of 12%.

A net present value of $0 would indicate that a project is expected to earn exactly the rate used to discount the future cash flows. If the net present value is a negative amount, the project will earn less than the rate used to discount the cash flows. (This doesn’t mean, however, that the project is showing a negative return—it could be the project is earning a return of 11% instead of the specified rate of 12%.)

4. Internal Rate of Return. This discounted cash flow model calculates the rate that will cause the net present value to equal zero. In other words, it answers the question, “What rate of return will the project earn over its life?” It is similar to the net present value method in that (a) all of the estimated cash flows over the entire life of the project are considered, and (b) the estimated cash flows are discounted to the present.

Since the internal rate of return model produces the rate that will discount all of the cash back to a net present value of exactly zero, you may need to try various rates (as shown in present value tables) until you find the exact rate that gives you zero. (You will save time by using a computer, financial calculator, or programmable calculator.)

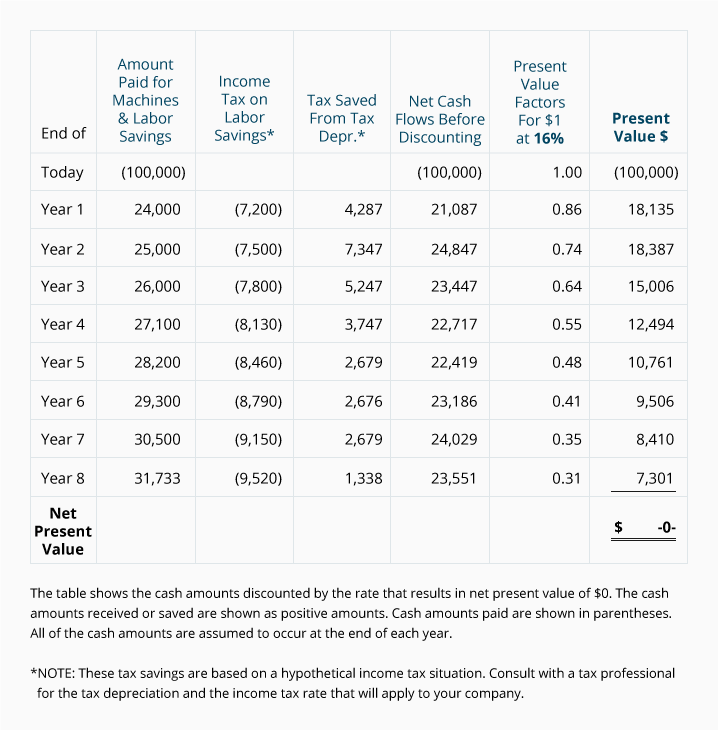
As you can see below, Treeline finds that a rate of 16% will yield a net present value of $0:

Knowing that the project has an internal rate of return of 16% may be more useful to Treeline than knowing its net present value is $14,668. In fact, if this method is applied to all of its capital expenditure proposals, Treeline can easily rank the proposals according to profitability. For example, if Treeline decides to commit no more than $500,000 for nonemergency projects, it can start by funding those proposals which show the highest internal rate of return and work its way down the list until the entire $500,000 is committed.

Another Application of a Present Value Calculation

A savvy company (or individual) will use the net present value method to help determine the amount it should spend to acquire another business. For example, assume that you wish to purchase Kirkland Co. You expect that the Kirkland Co. will generate positive net cash flows after tax of $15,000 per year for ten years, at which time you plan to liquidate or sell the company for $40,000 after taxes. To cover the risk associated with your investment in Kirkland Co. you need to earn 14%. With that in mind, what is the maximum amount you should pay today for Kirkland Co.?

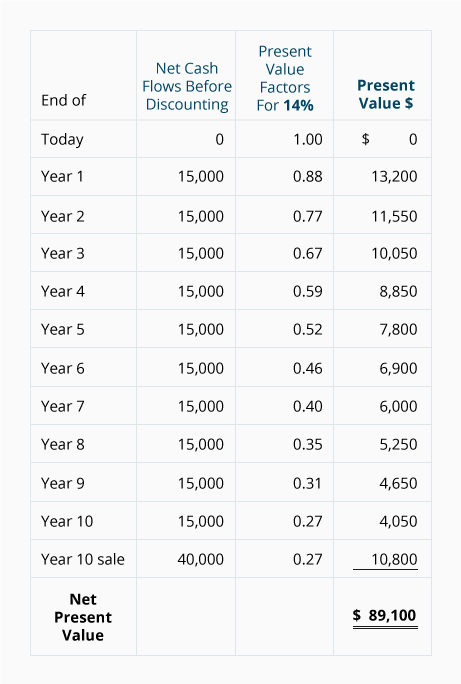
The net present value method will give us the amount to be paid in order to earn 14%. The following table shows the required calculations:

If you purchase the Kirkland Co. for $89,100 you will earn exactly a 14% return if the cash flows occur as estimated. If you pay more than $89,100 you will earn less than a 14% return; a price of less than $89,100 means you will earn more than a 14% return.

To learn the rate that you will earn on a specific price, you can compute the internal rate of return. This is done by finding the rate that will discount the future cash amounts back to the price.